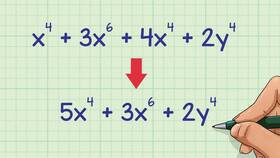Вычисление суммы степеней чисел - распространенная математическая операция, применяемая в различных областях. Рассмотрим основные методы решения таких задач.
Содержание
Вычисление суммы степеней чисел - распространенная математическая операция, применяемая в различных областях. Рассмотрим основные методы решения таких задач.
Основные понятия
- Степень числа: an = a × a × ... × a (n раз)
- Сумма степеней: S = a1k + a2k + ... + ank
- Натуральная степень: k ∈ N
Методы вычисления суммы степеней
| Тип суммы | Формула | Пример |
| Сумма квадратов | ∑i2 = n(n+1)(2n+1)/6 | 12+22+32 = 14 |
| Сумма кубов | ∑i3 = [n(n+1)/2]2 | 13+23+33 = 36 |
| Геометрическая прогрессия | ∑ark = a(1-rn)/(1-r) | 2+4+8 = 14 (a=2, r=2) |
Пошаговый алгоритм вычисления
1. Для последовательных натуральных чисел
- Определите количество слагаемых (n)
- Выберите соответствующую формулу для степени k
- Подставьте значения в формулу
- Выполните вычисления
2. Для произвольных чисел
- Возведите каждое число в требуемую степень
- Сложите полученные результаты
- Используйте калькулятор для больших чисел
Примеры расчетов
| Задача | Решение | Результат |
| 12+22+32+42 | 4×5×9/6 | 30 |
| 13+23+33+43 | (4×5/2)2 | 100 |
| 20+21+22+23 | (24-1)/(2-1) | 15 |
Частные случаи
Сумма одинаковых степеней
Для n одинаковых чисел: S = n × ak
Бином Ньютона
(a+b)n = ∑C(n,k)an-kbk
Полезные советы
- Для больших n используйте формулы вместо пошагового сложения
- Проверяйте правильность расчетов обратными вычислениями
- При работе с дробными степенями учитывайте область определения
Вычисление суммы степеней требует понимания математических закономерностей и правильного применения формул. Выбор метода зависит от конкретной задачи и вида степенного ряда.
