Сумма углов многоугольника - это важная геометрическая характеристика, показывающая общую величину всех внутренних углов данной фигуры. Это значение зависит от количества сторон многоугольника и подчиняется строгой математической закономерности.
Содержание
Формула суммы внутренних углов
Для выпуклого n-угольника сумма внутренних углов (S) вычисляется по формуле:
S = (n - 2) × 180°
где n - количество сторон (вершин) многоугольника.
Примеры для различных многоугольников
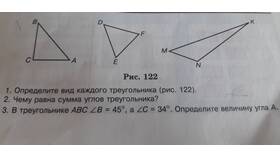
| Треугольник (3 стороны) | (3-2)×180° = 180° |
| Четырехугольник (4 стороны) | (4-2)×180° = 360° |
| Пятиугольник (5 сторон) | (5-2)×180° = 540° |
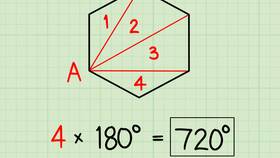
| Шестиугольник (6 сторон) | (6-2)×180° = 720° |
Доказательство формулы
Формула выводится следующим образом:
- Из любой вершины n-угольника проводим все возможные диагонали
- Многоугольник разбивается на (n-2) треугольника
- Сумма углов каждого треугольника равна 180°
- Общая сумма углов равна (n-2)×180°
Сумма внешних углов многоугольника
Для любого выпуклого многоугольника сумма внешних углов (по одному при каждой вершине) всегда равна 360°, независимо от количества сторон.
Практическое применение
- Построение геометрических фигур
- Решение задач на вычисление неизвестных углов
- Проверка правильности чертежей
- Архитектурные расчеты
- Компьютерная графика и 3D-моделирование
Особые случаи
- Для правильных многоугольников все внутренние углы равны между собой
- В случае невыпуклых многоугольников формула также остается справедливой
- Для звездчатых многоугольников применяются модифицированные формулы