Сумма внутренних углов любого выпуклого многоугольника может быть вычислена по универсальной формуле, зависящей от количества его сторон. Для четырнадцатиугольника (14-угольника) эта сумма имеет конкретное числовое значение.
Содержание
Сумма внутренних углов любого выпуклого многоугольника может быть вычислена по универсальной формуле, зависящей от количества его сторон. Для четырнадцатиугольника (14-угольника) эта сумма имеет конкретное числовое значение.
Формула для вычисления суммы углов
Сумма внутренних углов выпуклого n-угольника вычисляется по формуле:
S = (n - 2) × 180°
где n - количество сторон многоугольника.
Расчет для четырнадцатиугольника
Подставляя n = 14 в формулу, получаем:
- S = (14 - 2) × 180°
- S = 12 × 180°
- S = 2160°
Проверка на примерах
| Многоугольник | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | 180° |
| Четырехугольник | 4 | 360° |
| Пятиугольник | 5 | 540° |
| Четырнадцатиугольник | 14 | 2160° |
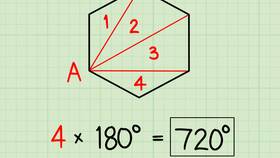
Геометрическое обоснование
Формула основана на том, что любой выпуклый n-угольник можно разбить на (n - 2) треугольника. Поскольку сумма углов каждого треугольника равна 180°, общая сумма углов многоугольника составляет (n - 2) × 180°.
Для четырнадцатиугольника:
- Количество треугольников при разбиении: 14 - 2 = 12
- Сумма углов: 12 × 180° = 2160°
Свойства выпуклого четырнадцатиугольника
- Все внутренние углы меньше 180°
- Диагонали лежат внутри многоугольника
- Любая прямая пересекает его не более чем в двух точках
- Количество диагоналей: 14×(14-3)/2 = 77
Вычисление одного угла правильного четырнадцатиугольника
В правильном четырнадцатиугольнике все углы равны. Чтобы найти величину одного угла:
- Общая сумма углов: 2160°
- Количество углов: 14
- Один угол: 2160° ÷ 14 ≈ 154,2857°
Применение знания суммы углов
Знание суммы углов четырнадцатиугольника полезно для:
- Решение геометрических задач
- Проектирование архитектурных сооружений
- Создание компьютерной графики
- Разработка дизайнерских решений
