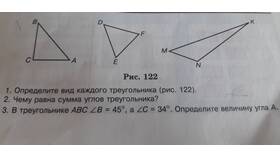
Одной из фундаментальных теорем в геометрии является теорема о сумме углов треугольника. Это знание имеет важное значение для решения множества геометрических задач.
Содержание
Одной из фундаментальных теорем в геометрии является теорема о сумме углов треугольника. Это знание имеет важное значение для решения множества геометрических задач.
Формулировка теоремы
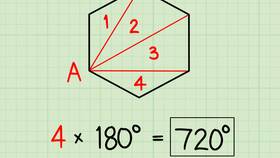
Сумма внутренних углов любого треугольника всегда равна 180 градусам (или π радианам). Это утверждение справедливо для всех типов треугольников на плоскости.
Доказательство теоремы
Классическое доказательство
- Рассмотрим произвольный треугольник ABC
- Проведем через вершину B прямую, параллельную стороне AC
- Образовавшиеся углы при точке B будут равны углам A и C соответственно
- Сумма углов на прямой равна 180°, следовательно, ∠A + ∠B + ∠C = 180°
Примеры расчета
| Тип треугольника | Углы | Сумма |
| Равносторонний | 60° + 60° + 60° | 180° |
| Прямоугольный | 90° + 45° + 45° | 180° |
| Тупоугольный | 100° + 40° + 40° | 180° |
Практическое применение
- Определение неизвестного угла треугольника
- Проверка корректности построения геометрических фигур
- Решение задач на построение
- Доказательство других геометрических теорем
Как найти неизвестный угол
Если известны два угла треугольника, третий можно найти по формуле:
∠C = 180° - (∠A + ∠B)
Исключения и особенности
Теорема справедлива только для плоских треугольников. В сферической геометрии сумма углов треугольника всегда больше 180°, а в гиперболической - меньше 180°.
Знание этой теоремы является базовым для дальнейшего изучения геометрии и находит применение во многих областях, включая архитектуру, инженерию и компьютерную графику.
